Vamos a profundizar sobre el modelo de valoración de activos financieros. El objetivo es conocer en qué consiste el modelo CAPM y realizar un ejemplo para una mayor comprensión.
Introducción
Podemos entender el modelo CAPM como un modelo de estudio y valoración de activos financieros que fue creado por William Sharpe. Este modelo estima la rentabilidad esperada según el nivel de riesgo. Consiste en un modelo teórico que se basa en el equilibrio del mercado. Es decir, asume la igualdad entre la oferta de activos financieros y su demanda.
Formulación CAPM
La interacción entre la oferta y la demanda va a establecer el precio de los activos. Debido a que la situación del mercado consiste en una competencia perfecta. Además, la rentabilidad del activo y el riesgo asumido manifiestan una situación de relación directa. Entendiendo la relación como a mayor riesgo, mayor rentabilidad.
De tal modo que, si otorgásemos valores al nivel de riesgo asumido, podríamos averiguar el porcentaje concreto de rentabilidad potencial de los activos. Debemos recordar que el modelo CAPM, solo tiene en cuenta el riesgo sistemático. Sin embargo, el riesgo total de un activo financiero también incluye el riesgo no sistemático o intrínseco del título determinado.
Este modelo intenta formular este razonamiento, considerando que se puede estimar la rentabilidad de un activo a través de la siguiente fórmula:
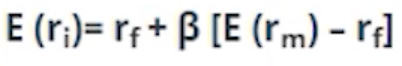
Explicación de la formulación CAPM
La primera parte de la fórmula (antes del signo de sumar) hace referencia al riesgo que se asocia al activo en concreto. Y, la segunda parte (después del signo de sumar) hace referencia al riesgo que se asocia al mercado en el que cotiza el activo.
Donde r sub i sería la tasa de rentabilidad esperada de un activo concreto. R sub f sería la rentabilidad del activo sin riesgo. Aunque todos los activos tienen un riesgo, se busca aquel que minimice el riesgo que, en escenarios de normalidad, son los activos de deuda pública. Por otro lado, encontramos la beta del activo financiero, que es la medida de la sensibilidad del activo en relación con su Benchmark.
Esta interpretación posibilita conocer la variación relativa de la rentabilidad del activo dentro del mercado concreto. En este sentido, cuanto más alto sea Beta, más grande será el riesgo que asume el activo. Por tanto, si Beta es mayor a 1 su interpretación nos dice que el activo tiene mayor riesgo que el mercado.
Si beta es inferior a 1, la interpretación nos explica que el activo tiene un riesgo menor que el mercado, por tanto, es bajo riesgo. Y, si beta es igual a 1, el riesgo del activo es similar al del merado. Por ejemplo, si una acción del DOW JONES tiene una beta del 1,4, quiere decir que cuando el DOW JONES suba un 10%, la acción aumentará un 14%. Por último, E(rm) hace alusión a la tasa de rentabilidad esperada dentro del mercado donde interacciona.
Si descomponemos la formulación anterior, podemos encontrar dos factores: r sub m menos r sub f sería el riesgo asociado al mercado de cotización. Y r sub i menos r sub f sería el riesgo asociado al activo determinado.
Por tanto, concluimos que la rentabilidad esperada del activo se especificará mediante el valor de beta como medición del riesgo sistemático.
Ejemplo práctico
Tras analizar el contenido teórico y práctico del presente modelo, a continuación, vamos a tratar un ejemplo práctico de aplicación de la fórmula
Hallar la tasa de rentabilidad esperada para el próximo año de la acción “Y” que cotiza en el DOW JONES. Disponiendo de los datos siguientes:
-Letras del tesoro (a un año) = rentabilidad del 2,5%. Supongamos que este activo concreto muestra una tasa de libre riesgo. Por tanto, rf=2,5%.
-El DOW JONES presenta una rentabilidad del 10% para el próximo ejercicio económico. Por tanto, E(rm)= 10%.
Y la beta de la acción “Y” respecto al DOW JONES es de 1,5. Es decir, la acción Y tiene un 50% más de riesgo sistemático que el DOW JONES.
Si aplicamos la fórmula anterior del modelo CAPM, obtendremos que la rentabilidad esperada estimada de la acción Y es del 13,75%.
Importancia del cálculo del modelo CAPM
En conclusión, el modelo CAPM, como modelo de valoración de activos financieros, es de gran utilidad. Puesto que va a perseguir el cálculo de la rentabilidad esperada, siempre en función del riesgo sistemático. Y, conseguir esta información es un proceso altamente valorado para las empresas.
En este sentido, puede ahorrar costes y la activación de planes de contingencia en la realización de determinados proyectos. Sobre todo, en aquellos en los que los márgenes son ajustados y cualquier desviación puede suponer un gran problema.
Para más información sobre este fenómeno y otros se puede acudir al Curso Experto en Análisis Técnico Bursátil y Gestión de Carteras de Renta Variable con la motivación de adoptar las claves del funcionamiento del modelo de valoración de activos en el mercado financiero, las claves de éxito y su repercusión.









Deja un comentario